Гармонический трейдинг
Мы уже говорили о том, что в основе импульсивных гармонических моделей должен лежать сетап с базовой конструкцией Z. Именно этот факт является определяющим в процессе идентификации и обозначения гармонических волновых конфигураций. Однако, ввиду наличия существенного субъективизма при волновой разметке, в процессе выделения гармонических конструкций иной раз бывает достаточно сложно однозначно сказать, что это за модель представлена на графиках.
Обычно, это присуще очень сложным гармоническим моделям, поэтому, в этих случаях приходится считать количество волн, и уже потом, по матрице, определять тип формации. Но об этом чуть позже. Итак, как показано в предыдущей таблице, количество волн в моделях второго порядка должно всегда соответствовать одному из чисел представленного ниже ряда. Берем формулу, и по ней вычисляем.
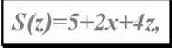
где: x - Количество трех волновых вложений,
z - Количество пяти волновых вложений.
Если в качестве примера рассмотреть правильную гармоническую волновую формацию xZ(z)x, то согласно данной формуле получим:
S(z)=5+2*2+4*1=13 волн.
Как упражнение по закреплению пройденного материала, попробуйте самостоятельно нарисовать эту гармоническую формацию, и убедитесь в правильности наших расчетов.
Импульсивные гармонические модели 2
Далее обратим внимание на таблицу импульсивных гармонических структур, приведенную ниже. Легко заметить, что в ней указаны только правильные модели, а именно, модели с симметричной волновой структ
Импульсивные гармонические модели 3
Для этого отмечу, что красными символами на самой верхней строке матрицы указаны разновидности «внутренних» вложений – ноль (или пусто), х, z. То же самое, расположено в первом столбце матрицы, но
Сетапы гармонических моделей
Уже неоднократно говорилось, что сетапы гармонических моделей, представляют собой одну из базовых конструкций, лежащей в основе гармонической структуры, с возможными вложениями внутри. В этом разд
Модель Z
Первый сетап, который мы рассмотрим, - будет базовая конструкция Z. Исходя из предыдущего материала, мы знаем, что модель Z представляет собой пяти волновую модель, которая лежит в основе огромног
Модель Z 2
Эта модель, одна из центральных структур волнового анализа. Так же мы знаем, что эта пяти волновая формация, с точки зрения «матрицы импульсивных структур», является ничем иным, как обычным Z - се
Модель Z 3
Возвращаясь к модели, отмечу, что в процессе торговли, я замечал различные варианты этой формации, в том числе случаи, где центральная структура может иметь различные формы: растянутую или, наобор
Модель Z 4
Такой фактор усложняет как саму модель, так и снижает качество прогнозирования с помощью гармонического волнового анализа. Давайте рассмотрим эти особенности. Сжатая модель Z очень часто может быт
Модель Z 5
Однако если взглянуть внимательно на саму фигуру, которую, я обычно выделяю эллипсом или кружком, то можно заметить ее разбиение на две, а не на одну, как должно быть, внутреннюю коррекционную вол
Модель Z 6
Что же касается растянутой Z – модели, то она очень часто выступает в качестве базы для формирования дальнейшего ценового вложения. Именно у растянутых Z-моделей имеется максимальная вероятность,
Модель Z 7
Таким образом, в зависимости от того, по какому из сценариев происходит развитие сетапа, возникает возможность строить предпосылки о принадлежности формации к той или иной группе моделей, а так же
Модель Z(x)
Вторая по счету, разновидность гармонических сетапов, представляет собой модель Z(x). Запись данной гармонической структуры показывает, что в основе ее конструкции лежит обычная пяти волновая Z фо
Модель Z(x) 2
Еще одной ее особенностью, является тот факт, что эта конструкция достаточно часто встречается на графиках цен, и представляет собой, по сути, полную противоположность коррекционной формации xXx.
Модель Z(x) 3
Характерным примером этого случая, является апрельская ситуация 2007 года, когда на дневных графиках GBP/JPY, CHF/JPY была сформирована соответствующая модель, предсказывающая среднесрочный рост э
Модель Z(z)
Последняя, самая редкая разновидность сетапов, которую мне удалось несколько раз встречать на графиках цен, представляет собой симметричную, девяти волновую конструкцию Z(z). Если приглядеться вни
Модель Z(z) 2
Если, например, модели xXx или xZx встречаются практически повсеместно, то эту формацию мне с трудом удалось отыскать на графиках цен. Более того, как и в случае с предыдущим сетапом Z(x), нашел я
Модель Z(z) 3
Продолжая рассматривать тематику преобразования гармонических моделей, стоит упомянуть и о частой формации ZZ, которая по количеству волн напоминает рассмотренную нами модель Z(z). Моде
Модель Z(z) 4
Модель ZZ на недельном графике GBPUSD Если с конструкцией ZZ все понятно (они образуются в условиях параллельных каналов), то неправильная конфигурация Z(x)x наводит на некоторые размыш
Модель xZx
Одной из первых, гармонических волновых моделей, которую стоит внимательно изучить, является симметричная структура xZx. Ее особенность в том, что в качестве ядра у нее расположена базовая констру
Модель xZx 2
Сама по себе, эта модель представляет собой достаточно простое образование, и весьма часто встречается на графиках цен. Термин «вырожденная разновидность Z(x)» я специально употребил для того, что
Модель xZx 3
Обратите внимание, что модель xZx, сформированная на 4-х часовом графике британского фунта к американскому доллару, с одной стороны, предсказывает скорое начало роста, а с другой стороны, хорошо в
Модель xZ(x)x
Продолжая рассматривать особенности формирования импульсивных гармонических моделей, пришла пора, перейти к следующей, распространенной модели - одиннадцати волновой формации xZ(x)x. Она представл
Модель xZ(x)x 2
Итак, мы с вами рассмотрели закономерности, лежащие в основе формирования сложных гармонических волновых моделей, и определили последовательность возникновения конструкций на базе центральных Z -
Модель xZ(z)x
Следующей разновидностью сложных гармонических моделей, внешними вложениями которой выступают X-модели, является тринадцати волновая модель xZ(z)x. От предыдущей конструкции, ее отличает только фо
Модель xZ(z)x 2
Проанализировав ситуацию на рынке, я обратил внимание на то, что типичный нисходящий канал, сформированный на графике золота, представляет собой сложную гармоническую структуру xZ(z)x. К этому вре
Модель zZz
Пришло время, перейти к изучению более сложных гармонических моделей, которые не так уж просто обнаружить начинающим трейдерам. Тринадцати волновые модели, в том числе и конфигурацию zZz – я встре
Модель zZz 2
Весь медвежий участок цены, на 4-х часовом графике британского фунта по отношению к доллару (GBPUSD), являет собой данную сложную модель. Медвежья модель zZz на графике британского фунт
Microsoft Project 2003 для менеджеров
Project — программный продукт компании Microsoft, призванный помочь менеджерам и руководителям в управлении проектами. Программы Word, Excel и Outlook лишь отчасти способствуют автоматизации рабочего места менеджера, программа Project помогает решить эту проблему. При планировании проекта нужно составить список задач, требующих решения, и список ресурсов, которые могут в этом помочь, а затем назначить ресурсы задачам. На этапе осуществления проекта необходимо следить за ходом работы, сроками и затраченными средствами. Microsoft Project автоматизирует эти процессы.В России Microsoft Project используется не так давно, после появления версии 2002, хотя существует он уже почти 10 лет. На сегодняшний день последней версией является Microsoft Office Project Professional 2003. Кроме Professional существуют Project Standard, Server и Web Access. Это не значит, что данный раздел не подходит для изучения Microsoft Office Project Standard 2003 или какой-либо другой версии программы, просто между версиями могут быть некоторые различия. Хотя Project 2002 практически не отличается от 2003, так что раздел в каком-то смысле универсален. Рассмотрим версии программы Microsoft Office Project подробнее.
Общие сведения
Интерфейс
Главное меню
Дополнительные окна
Окна вставки и поиска
Консультант и система помощи
Основы создания проектов
Анализ
Приложения
