Решение системы линейных уравнений методом простой итерации
Циклические вычисления можно проводить и над массивами. В качестве примера такой задачи рассмотрим итеративный способ решения системы линейных уравнений AX = B. Если применить метод простой итерации, то вектор решений X определяется следующим рекуррентным соотношением:
XK+1 = XK -(AXK -B) k= 1…N
Чтобы запустить процесс вычислений, нужно задать начальное приближение - вектор X1. Для сходимости процесса необходимо, но не достаточно, чтобы норма матрицы А была меньше 1. Иногда достаточно соответствующим образом масштабировать матрицу А и вектор В. Но нас конечно интересуют другие вопросы,- как реализовать на Excel это итеративное соотношение над векторами и матрицами, не прибегая к программированию на VBA и используя циклические вычисления. Покажем, что решение получить ненамного сложнее, в сравнении с применением схемы Ньютона для одного уравнения. Я сделал следующее:
-
Ввел матрицу А и вектор В, предварительно нормировав их. Заметим, что нужно правильно выбирать ориентацию векторов. В данном случае мне было удобнее представлять вектор В строкой. Вектор получил имя Veb.
-
Затем определил вектор с именем Vxinit, задающий начальное приближение.
-
Затем определил еще один вектор с именем Vxcur. Это вектор решений, его значения будут изменяться в цикле, пока не закончится итерационный процесс. Формула для вычислений будет определяться написанным выше рекуррентным соотношением, и представлять собой формулу над массивами. Учитывая то, что говорилось ранее о рекуррентных соотношениях, формула должна быть IF - функцией. Это позволит использовать на первом шаге начальное приближение, а потом уже вести вычисления по рекуррентной формуле. Приведем теперь саму формулу над массивами, вычисляющую рекуррентно вектор Vxcur:
{=ЕСЛИ(Vxcur=0; Vxinit; Vxcur - Axhor + Veb)}
Здесь, как и ранее, используются нулевые значения, как признак начала процесса. Заметим, что, конечно, было бы лучше, если бы существовала возможность явной инициализации переменных при циклических вычислениях, а так наши действия немного напоминают фокус. Вектор Axhor, введенный в формулу - это вспомогательный вектор, равный произведению матрицы А на текущий вектор Vxcur. Если процесс вычислений сходится, и Vxcur сходится к решению системы уравнений, то вектор Axhor будет сходиться к вектору Veb.
-
Опишем подробнее формирование вспомогательного вектора Axhor. Содержательно, он представляет произведение матрицы на вектор. Но произведение матрицы на вектор дает вектор столбец, а в рекуррентном соотношении необходим вектор строка. По этой причине я формирую вначале вектор столбец Axver:
Axver = A*Vxcur
Конечно, для умножения матрицы на вектор можно воспользоваться стандартной функцией, но я хочу показать, как это делается с использованием более простых средств. Для этого достаточно написать формулу, вычисляющую его первый элемент:
{=SUM(A38:B38*Vxcur)}
и затем скопировать ее по столбцу. Обратите внимание, вектор, на который умножается матрица, должен быть строкой, а вектор - результат - столбцом. Строка матрицы задается в относительных адресах и при копировании меняется. Вектор, на который умножаются строки, задается своим именем, а значит абсолютным адресом, не изменяющимся при копировании. Каждая формула, задающая элемент вектора, является формулой над массивами.
Получив вектор столбец Axver, задающий нужное произведение, можно перейти к получению строки - Axhor, представляющей результат транспонирования вектора Axver. Для транспонирования я использовал стандартную функцию Transpose. Сама задача транспонирования и эта функция подробно будет рассмотрена чуть позже. Формула над массивами, определяющая вектор Axhor имеет вид:
{=ТРАНСП(Axver)}
Задав все вектора и все формулы, я получил решение системы линейных уравнений. Как ни странно, но даже столь плохой метод, как метод простой итерации сошелся к решению. Так, начав с начального приближения (1,1), я получил решение (1.6, 2.4) с заданной точностью.
Заметим, предложенная схема носит общий характер и позволяет решать любую систему линейных уравнений, не ограничиваясь системой из двух уравнений, рассмотренную в примере. Однако никому не рекомендую применять метод простой итерации для нахождения решения системы уравнений, - для этого есть другие точные методы. Просто мне было важно продемонстрировать возможность циклических вычислений при действиях с матрицами, и нужен был достаточно простой пример.
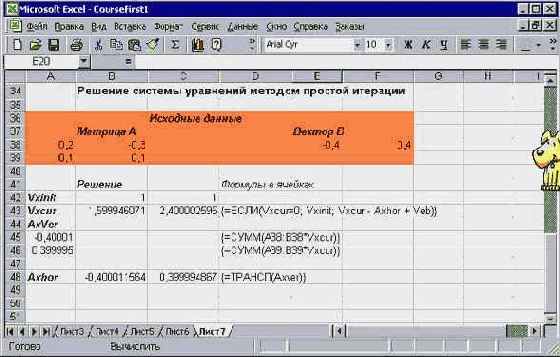
В заключение темы о циклических вычислениях покажем, как выглядят построенное решение на рабочем листе Excel:
увеличить изображение
Рис. 2.3. Циклические вычисления и действия над матрицами
Опишем подробнее формирование вспомогательного вектора Axhor. Содержательно, он представляет произведение матрицы на вектор. Но произведение матрицы на вектор дает вектор столбец, а в рекуррентном соотношении необходим вектор строка. По этой причине я формирую вначале вектор столбец Axver:
Axver = A*Vxcur
Конечно, для умножения матрицы на вектор можно воспользоваться стандартной функцией, но я хочу показать, как это делается с использованием более простых средств. Для этого достаточно написать формулу, вычисляющую его первый элемент:
{=SUM(A38:B38*Vxcur)}
и затем скопировать ее по столбцу. Обратите внимание, вектор, на который умножается матрица, должен быть строкой, а вектор - результат - столбцом. Строка матрицы задается в относительных адресах и при копировании меняется. Вектор, на который умножаются строки, задается своим именем, а значит абсолютным адресом, не изменяющимся при копировании. Каждая формула, задающая элемент вектора, является формулой над массивами.
Получив вектор столбец Axver, задающий нужное произведение, можно перейти к получению строки - Axhor, представляющей результат транспонирования вектора Axver. Для транспонирования я использовал стандартную функцию Transpose. Сама задача транспонирования и эта функция подробно будет рассмотрена чуть позже. Формула над массивами, определяющая вектор Axhor имеет вид:
{=ТРАНСП(Axver)}
Задав все вектора и все формулы, я получил решение системы линейных уравнений. Как ни странно, но даже столь плохой метод, как метод простой итерации сошелся к решению. Так, начав с начального приближения (1,1), я получил решение (1.6, 2.4) с заданной точностью.
Заметим, предложенная схема носит общий характер и позволяет решать любую систему линейных уравнений, не ограничиваясь системой из двух уравнений, рассмотренную в примере. Однако никому не рекомендую применять метод простой итерации для нахождения решения системы уравнений, - для этого есть другие точные методы. Просто мне было важно продемонстрировать возможность циклических вычислений при действиях с матрицами, и нужен был достаточно простой пример.
В заключение темы о циклических вычислениях покажем, как выглядят построенное решение на рабочем листе Excel:

увеличить изображение
Рис. 2.3. Циклические вычисления и действия над матрицами
